Interactive three-dimensional simulations & visualizations
Visualizing the beauty in physics and mathematics
Project maintained by zhendrikse Hosted on GitHub Pages — Theme by mattgraham
Particle and quantum physics
If you think you understand quantum mechanics, you don't understand quantum mechanics. — Richard P. Feynman
Plane waves & the particle in a box
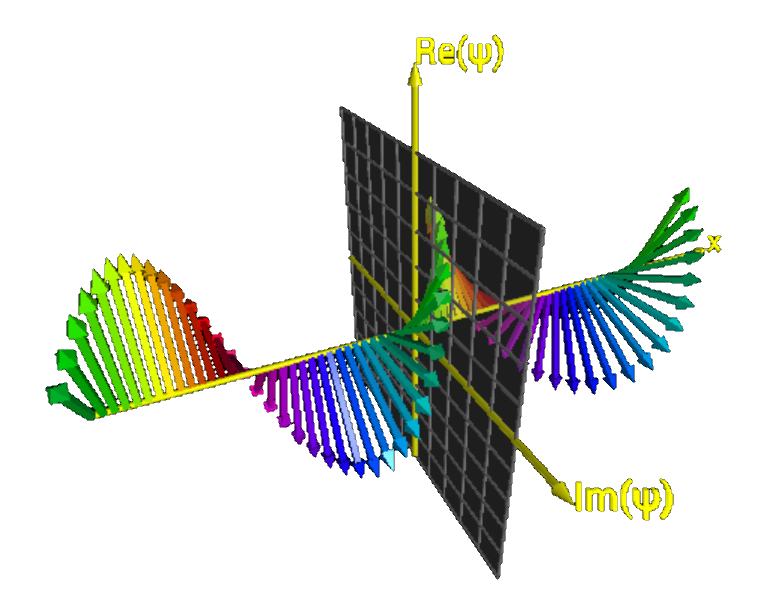
⇓ For a plane wave, we can easily derive the Schrödinger equation ⇑
According to De Broglie we have: $$p = \dfrac{h}{\lambda} = \dfrac{h}{2\pi} \dfrac{2\pi}{\lambda} = \hbar k \Rightarrow \hbar k = \hbar \dfrac{\partial}{\partial x} \psi(x,t) = p \psi(x, t) \Rightarrow p = \hbar \dfrac{\partial}{\partial x}$$ The Kinetic energy can be expressed as: $$K = \dfrac{p^2}{2m} = -\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial x^2} \psi(x,t)$$ The total energy is given by the Planck-Einstein relation: $$E = hf = \dfrac{h}{2\pi}\dfrac{2\pi}{T} = \hbar \omega \Rightarrow -i\hbar\dfrac{\partial}{\partial t} \psi(x,t) = E \psi(x,t) \Rightarrow E = -i\hbar\dfrac{\partial}{\partial t}$$ From this we arrive at the Schrödinger equation: $$(KE + PE)\Psi(x,,t) = E\Psi(x,t) = -i\hbar \dfrac{\partial}{\partial t}\Psi(x, t) = -\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial x^2} \Psi(x,t) + V(x)\Psi(x,t)$$ In three-dimensional space this is then generalized to: $$i\hbar\dfrac{\partial}{\partial t}\Psi(\vec{r}, t) = \left(-\frac{\hbar^2}{2m}\nabla^2 + V(\vec{r, t}\right)\Psi(\vec{r}, t)$$⇓ Background: particle in a box, i.e. confined by a infinite square well ⇑
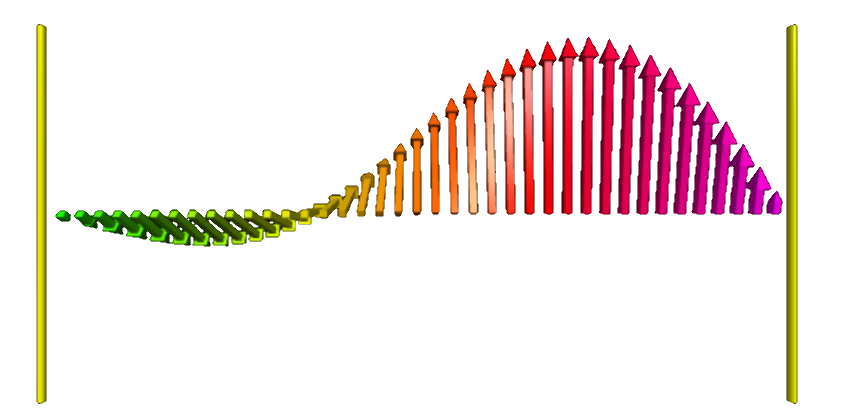
Although the one-dimensional particle-in-a-box problem does not correspond to any real-world system, it illustrates quite well some (fundamental) quantum mechanical features nonetheless.
The box is modeled by an infinite square well, so that the particle cannot escape beyond the boundaries of the box.
Inside the box, the potential energy $V$ is zero (or constant). Substituting this together with the formula for the plane wave $\psi(x,t) = Ae^{ik x}e^{-i\omega t}$ into the Schrödinger equation, we get: $$\dfrac{\partial^2\psi}{\partial x^2} + \dfrac{8\pi^2m}{h^2}(E - 0)\psi=0 \Rightarrow \bigg(\dfrac{-h^2}{8\pi^2m}\bigg)\dfrac{\partial^2\psi}{\partial x^2}=E\psi$$ Which function does give itself (times $E$) when differentiated twice _and_ is zero at both boundaries of the box? $$\psi = A\sin(ax) \Rightarrow \dfrac{h^2a^2}{8\pi^2m}\psi=E\psi \Rightarrow E=\dfrac{h^2a^2}{8\pi^2m}$$ To get $a$, we note that the wave function equals zero at the box boundaries: $$\psi=A\sin(ax) = 0 \Rightarrow a=\dfrac{n\pi}{L} \Rightarrow \psi_n = A\sin\bigg(\dfrac{n\pi x}{L}\bigg) \Rightarrow E_n=\dfrac{h^2n^2}{8mL^2}$$ Normalizing the wave function results in an expression for $A$: $$\int_0^L \psi \cdot \psi dx = 1 \Rightarrow A^2 \int_0^L\sin^2\bigg(\dfrac{n\pi x}{L}\bigg) dx=1 \Rightarrow A^2\bigg(\dfrac{L}{2}\bigg)=1 \Rightarrow A=\sqrt{\dfrac{2}{L}}$$ So summarizing, we have $$E=\dfrac{h^2a^2}{8\pi^2m} \text{ and } \psi_n=\sqrt{\dfrac{2}{L}}\sin(nkx), \text{where } k=\dfrac{\pi}{L}$$ These energy eigenstates (and superpositions thereof) are used in the visualization software.The quantum harmonic oscillator
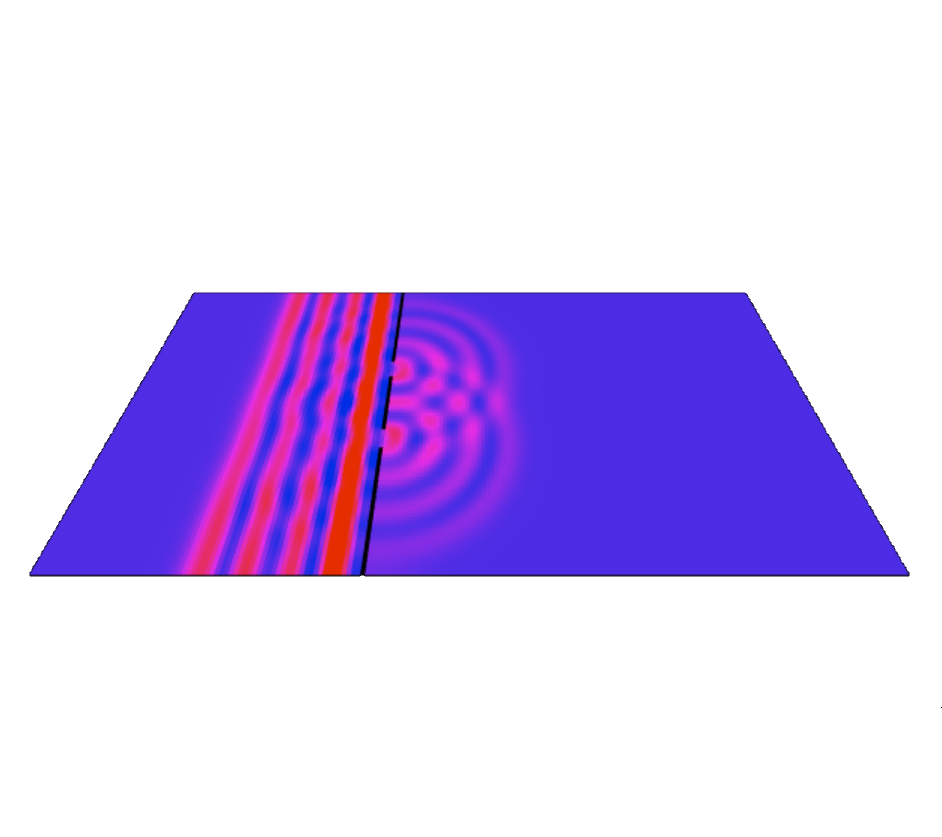
Young's interference experiment

Share on: