Interactive three-dimensional simulations & visualizations

Visualizing the beauty in physics and mathematics

Project maintained by zhendrikse Hosted on GitHub Pages — Theme by mattgraham

Zeger's home / Science home / Mathematics /

Chaos game

The chaos game is an iterative procedure $s_i\rightarrow s_{i+1}$ that can be written as an affine transformation

$s_{i+1}=T_js_i+r_j$

where the set of pairs {$(T_j, r_j) | j=1,2,\dots$} with matrices $T_j$ and $r_j$ characterize the chosen ruleset and $j$ denotes a (per iteration) randomly chosen index. The famous Barnsley fern is generated in a similar way.

This chaos_game.html is 100% Javascript, written by Zeger Hendrikse
Inspired by nnakul/chaos-game by Nikhil Nakul
A VPython version is available as well, see chaos_game.py

Cantor dust	Fractal star
Fractal flower	Sierpinski carpet
Sierpinski triangle	T-square fractal
Vicsek fractal

Why do fractals arise from the chaos game

The chaos game is an iterative process of placing dots on a canvas using certain fixed locations (vertices) that are chosen randomly. For example, in the animation below, the position of each new dot is halfway between the current position and one of the three fixed corners of a triangle.

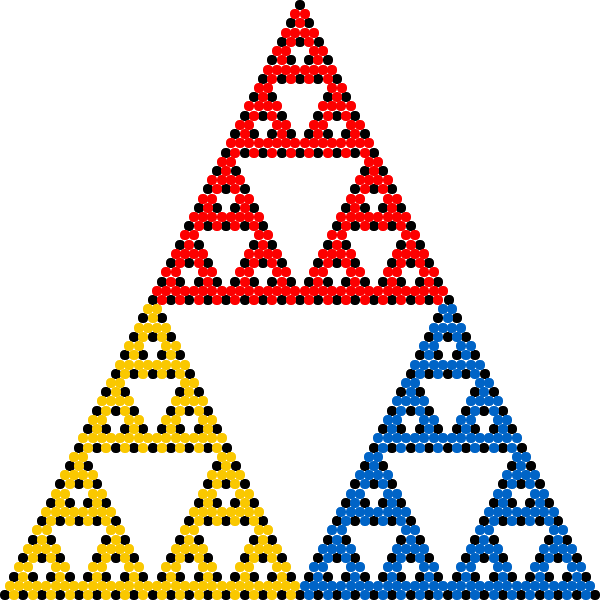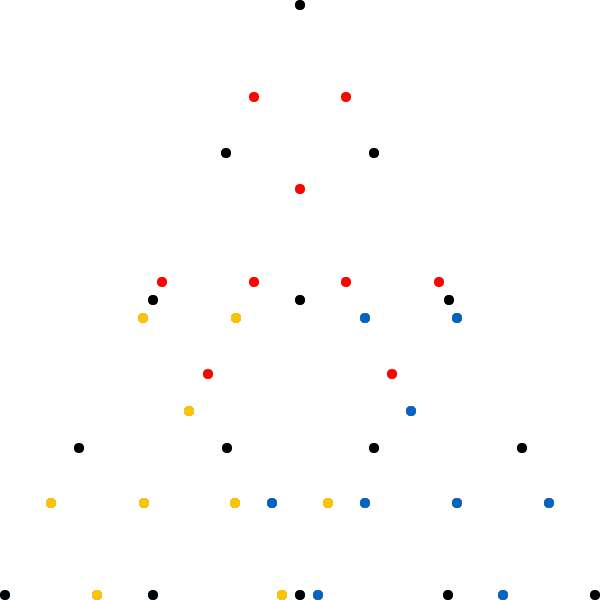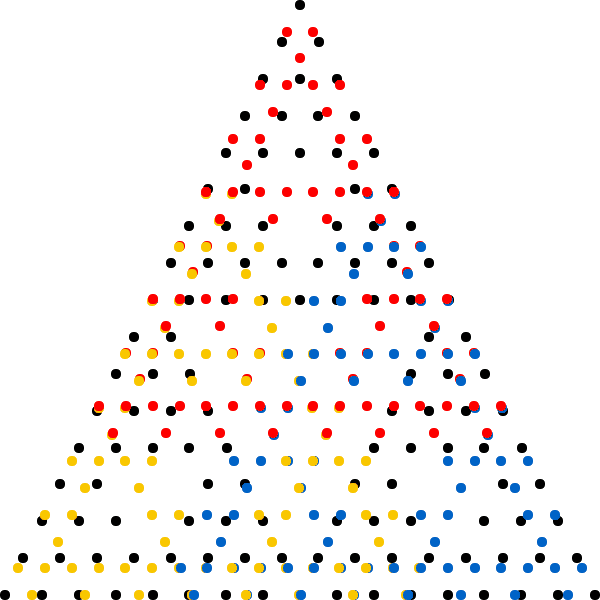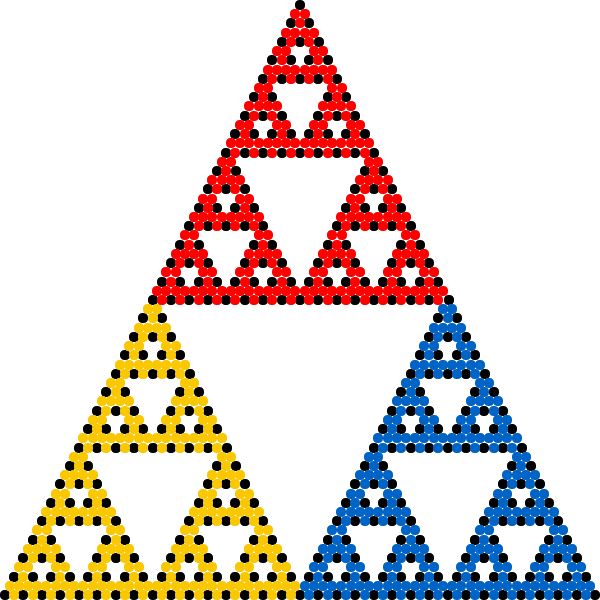
Let’s assume we start with a point that is located in one of the areas that will eventually be empty, see the figure below.

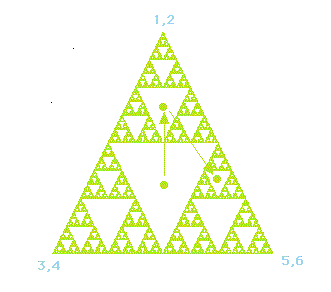
After one iteration, the point will jump to either one of the three smaller empty triangles. Eventually after a couple of iterations, the point will enter a small triangle that is so small that, given the finite resolution of the screen and the pixels it contains, it will disappear.

In a certain sense, the fractal itself is a kind of strange attractor!

Example Python code

jump_points = [(-.5, .433), (.5, -.433), (0, .3)] # triangle vertices
colors = [color.green, color.cyan, color.red] 

for i in range(40000):
    index = int(random() * 3) # random vertex to jump to
    x = .5 * (x + jump_points[index][0])
    y = .5 * (y + jump_points[index][1])
    pixels.append(pos=vec(x, y, 0), color=colors[index])

References

Share on: