Interactive three-dimensional simulations & visualizations
Visualizing the beauty in physics and mathematics
Project maintained by zhendrikse Hosted on GitHub Pages — Theme by mattgraham
Rendering a black hole using ray tracing
- Based on the blackhole_raytracer project by Arman T, Casper Y, Lulu W.
- See their accompanying GitHub pages and video, where they explain the code.
- This black hole ray tracer is a port to Javascript executed by a web worker.
- Refactored and extended with realistic colour coding by Zeger Hendrikse.
- A VPython version is also available as black_hole_raytracer.py.
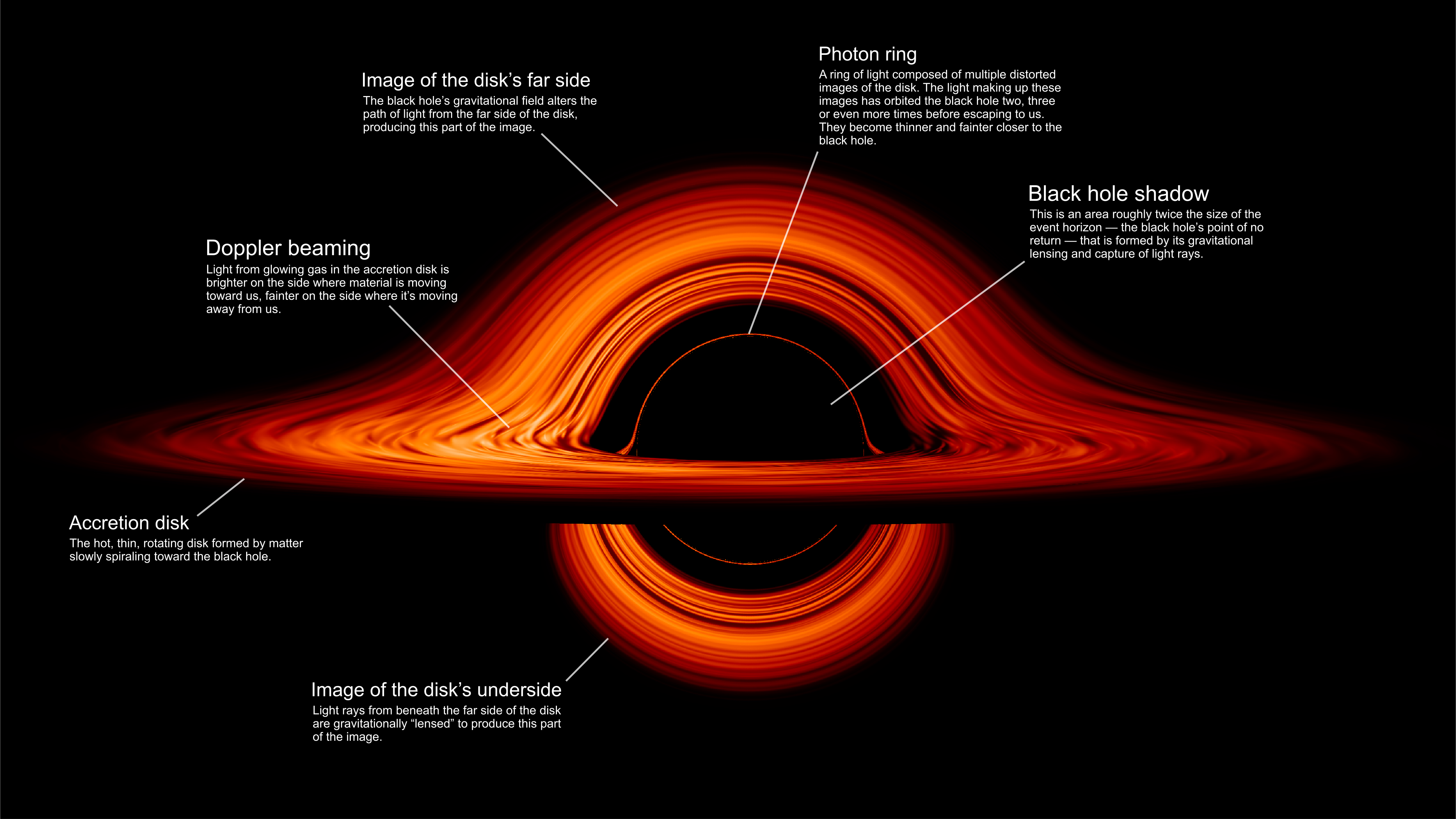
Image rendition explained
Real images of black holes
For comparison, below are some real images of black holes, showing a bright ring formed as light bends in the intense gravity around a black hole.



A concise history
Black holes are an outcome of the Einstein field equations (EFE):
$R_{\mu\nu} -\frac{1}{2}R G_{\mu\nu} + \lambda g_{\mu\nu} = k T_{\mu\nu}$
The expression on the left represents the curvature of spacetime as determined by the metric; the expression on the right represents the stress–energy–momentum content of spacetime. The EFE can then be interpreted as a set of equations dictating how stress–energy–momentum determines the curvature of spacetime.
[…]
The equations are more complex than they appear. Given a specified distribution of matter and energy in the form of a stress–energy tensor, the EFE are understood to be equations for the metric tensor $g_{\mu\nu}$, since both the Ricci tensor and scalar curvature depend on the metric in a complicated nonlinear manner. When fully written out, the EFE are a system of ten coupled, nonlinear, hyperbolic-elliptic partial differential equations. — Wikipedia
This led John Archibald Wheeler, the “hero of the black hole story” according to Steven Hawking and the first to coin the term black hole, to state that
Spacetime tells matter how to move; matter tells spacetime how to curve.
Back in 1915, Karl Schwarzschild was the first to actually derive an exact solution to these equations, which is quite an achievement, even more so when you consider that he accomplished this feat while he was serving in the German army during World War I. He left clues in his work, clues that are now known as the Schwarzschild radius and the existence of singularities.
Around the same time, Einstein was theorizing about the existence of what we now call black holes, when he tried to prove that celestial objects that are so dense that their gravity prevents even light from escaping, could not exist.
But in 1939, physicists J. Robert Oppenheimer (about whom the famous movie was made) and Hartland Snyder published a paper called “On Continued Gravitational Contraction”, which provided a solution to the EFE based on the Schwarzschild metric, which describes the collapse of an extremely massive object into a black hole.

Share on: