Interactive three-dimensional simulations & visualizations

Visualizing the beauty in physics and mathematics

Project maintained by zhendrikse Hosted on GitHub Pages — Theme by mattgraham

Vector fields & implied flow



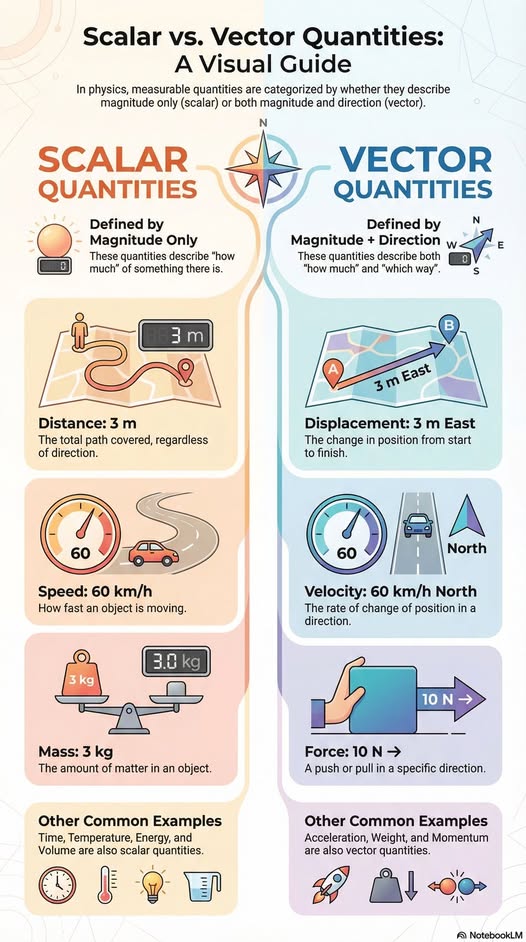
Scalar vis-à-vis vector quantities


Scalar versus Vector Quantities
This excellent visual guide originates from House of Physics.

What do the colors show?


Given a vector field $F = (u, v, w)$, the divergence is defined by

\[\nabla \cdot \mathbf{F} = \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z}\]

Interpretation:

🔴 positive → source
🔵 negative → sink
⚪ zero → incompressible

The curl is defined by

\[\nabla \times \mathbf{F}\]

For the color we use the magnitude of the curl: \(||\nabla \times \mathbf{F}||\)

Interpretation:

The vector field is sampled on a lattice, so we apply central differences.

For the divergence this leads to

∂u/∂x ≈ (u(x+dx) − u(x−dx)) / (2dx)
∂u/∂y ≈ (u(y+dy) − u(y−dy)) / (2dy)
∂u/∂z ≈ (u(z+dz) − u(z−dz)) / (2dz)

and the curl

curl_x = ∂w/∂y − ∂v/∂z
curl_y = ∂u/∂z − ∂w/∂x
curl_z = ∂v/∂x − ∂u/∂y

Summarizing:

Property Channel
Direction Arrow orientation
Strength length
Divergence color
Rotation curl-color
Time animation

Possible extensions

In the future, the following may be added:

🧭 streamlines / pathlines
🧠 Helmholtz-decompositie
📊 interactieve colorbar
âš¡ GPU finite differences (shader)
🌀 curl-vectors as opposed to magnitude


Share on: