Interactive three-dimensional simulations & visualizations

Visualizing the beauty in physics and mathematics

Project maintained by zhendrikse Hosted on GitHub Pages — Theme by mattgraham

Divergence and curl demo


What are you looking at?

This is a dynamic particle and vector field simulation where points interact with sources, sinks, and swirling currents. Every particle moves according to the invisible forces around it, tracing the flow of this small, colorful universe.

Click on the canvas to start the animation and watch the field come alive!

Click to bring the flow to life!

⭐ Original idea by Let's code physics
🔧 Ported to div_curl_demo.html by Zeger Hendrikse
👉 A VPython version is also available as div_curl_demo.py.

Scalar vis-à-vis vector quantities


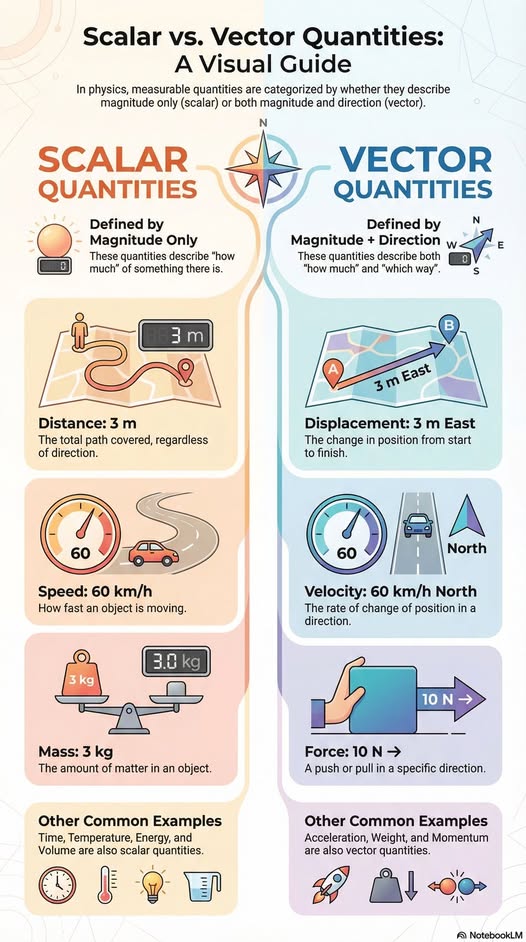
Scalar versus Vector Quantities
This excellent visual guide originates from House of Physics.

Background information


\[\text{Divergence: }\vec{\nabla} =\begin{pmatrix} \partial/\partial x \\ \partial/\partial y \\ \partial/\partial y \end{pmatrix} \Rightarrow \vec{\nabla} \cdot \vec{V} = \dfrac{\partial V_x}{\partial x} + \dfrac{\partial V_y}{\partial y} + \dfrac{\partial V_z}{\partial z}\] \[\text{Curl: } \vec{\nabla} \times \vec{V} = \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ V_x & V_y & v_z \end{vmatrix} = \begin{pmatrix} \partial V_z/\partial y - \partial F_y/\partial z \\ \partial V_x/\partial z - \partial F_z/\partial x \\ \partial V_y/\partial x - \partial F_x/\partial y\end{pmatrix}\]

Share on: